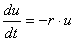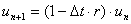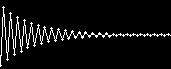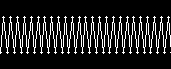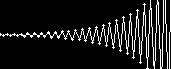微分方程式と差分方程式(漸化式)
文責:尾崎 淳
微分形式から差分形式(漸化式)へ
漸化式の基本は等差数列と等比数列だと言ったが、さらにまとめると、基礎中の基礎は等差数列の方である。
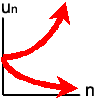
| 漸化式 | 一般項 | 解の振る舞い | |
| 等差数列 | 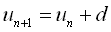 |
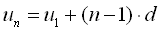 |
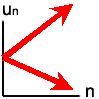 |
| 等比数列 | 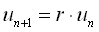 |
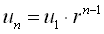 |
 |
一般に、ある量uの時間変化の式は、
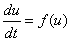 |
(1) |
と書ける。f(u)が正ならば増加、負ならば減少である。 ここで左辺を
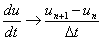 |
とおくことにより微分(連続)から差分(離散)へと近似できる(Δtは時間刻み)。 式を整理すると、
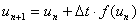 |
(2) |
この式は右辺に時刻nの値unを代入すると、次の時刻n+1の値un+1が得られるようになっている。 シミュレーションでは、この式を使って繰り返し計算(u1を代入してu2を計算→u2を代入してu3を計算→・・・)を行っている。
ここでΔt·f(u) ⇒ dとおいてみると(2)式は、形式上、等差数列であることがわかる。
つまり全ての基本は等差数列である。
まず、イメージがはっきりと湧く“ひな形”の式を持ちましょう。
数式の形なんて無限にあります。
式ごとに別の概念をあてはめるのではなく、基本となる“ひな形”に置き換えるのです。
そうすれば一見オニのような式でも大したことを言っていないことが分かります。つまるところ結局みんな反応拡散!だとわかるさ、きっと。
等比数列とは、公差dが変動する等差数列である
化学反応は普通、分子の濃度依存的に起こる。そこで最も単純に、変化率が濃度に比例する形 r·u をとり、これを等差数列の式に入れると、
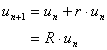 |
となり、等比数列の式ができる。ここで R = 1+r とおいた。
シミュレーションする際の注意点
ここで注意しなければいけないことがある。
微分形式では変化率は“r”と書いたが、漸化式では“1+r”である。
つまり、よく微分形式と差分形式とを並列に記述することが多いが、差分形式(漸化式)はむしろ“積分形式”だと言ったほうが良い(だからシミュレーションできるのだ)。
当ページでも振動現象を説明するのに
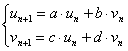 |
を使ったが、正確には
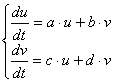 |
⇔ | 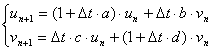 |
である。 ただし、ここでは厳密さよりもイメージを大切にしたいので簡略化した。 矢印を書くのに“1”とか“Δt”とかは本質じゃないでしょ。かえって訳わかんなくなる。
|
|
||||||||||||||||
.gif) |